如图,在网格中有一个四边形的图案。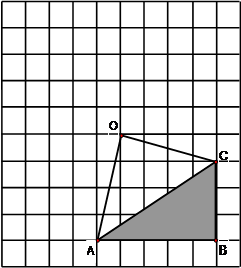
请你画出此图案绕点O顺时针方向旋转90°,180°,270°的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错;
若网格中每个小正方形的边长为1,旋转后点
 的对应点依次为
的对应点依次为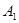 ,
,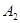 ,
,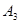 ,求四边形
,求四边形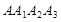 的面积;
的面积;这个美丽图案能够证明一个我们学过的著名定理,请直接写出这个定理名称,不要求证明。
相关知识点
推荐套卷
如图,在网格中有一个四边形的图案。
请你画出此图案绕点O顺时针方向旋转90°,180°,270°的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错;
若网格中每个小正方形的边长为1,旋转后点
 的对应点依次为
的对应点依次为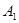 ,
,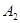 ,
,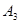 ,求四边形
,求四边形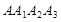 的面积;
的面积;这个美丽图案能够证明一个我们学过的著名定理,请直接写出这个定理名称,不要求证明。