在四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=A，AB=2，以AC的中点O为球心、AC为直径的球面交PD于点M。
（1）求证：平面ABM⊥平面PCD；
（2）求直线CD与平面ACM所成的角的大小；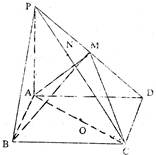
相关试题
的图象关于原点成中心对称, 试判断
在区间
上的单调性,并证明你的结论.
若（
UA）
（
求
。
的前n项和
与通项
之间满足关系
求
，求
的前n项和
（本小题13分）
定义在R上的函数
满足：如果对任意
，都有
，则称是R上凹函数。已知二次函数
（
）。
（1）求证：当
时，函数为凹函数；
（2）如果
时，
，试求a的取值范围。
对任意
都有
求
和
的值；
数列
满足：
=
+
，数列
是等差数列吗？请给予证明；推荐套卷
在四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=A，AB=2，以AC的中点O为球心、AC为直径的球面交PD于点M。
（1）求证：平面ABM⊥平面PCD；
（2）求直线CD与平面ACM所成的角的大小；
（本小题13分）
定义在R上的函数满足：如果对任意，都有，则称是R上凹函数。已知二次函数（）。
（1）求证：当时，函数为凹函数；
（2）如果时，，试求a的取值范围。
粤公网安备 44130202000953号