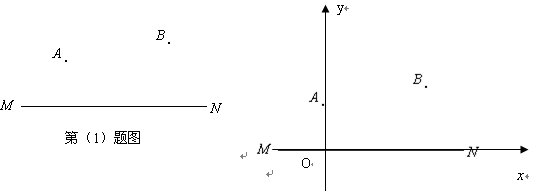
如图,要在公路M N旁修建一个货物中转站P,分别向A、B两个开发区运货。(分别在图上找出点P,并保留作图痕迹.)若要求货站到A、B两个开发区的距离相等,那么货站应建在那里?
若要求货站到A、B两个开发区的距离和最小,那么货站应建在那里?如图(2)建立平面直角坐标系,若已知A(0,2),B(4,3),请求出相应的P点坐标。
相关知识点
推荐套卷
如图,要在公路M N旁修建一个货物中转站P,分别向A、B两个开发区运货。(分别在图上找出点P,并保留作图痕迹.)若要求货站到A、B两个开发区的距离相等,那么货站应建在那里?
若要求货站到A、B两个开发区的距离和最小,那么货站应建在那里?如图(2)建立平面直角坐标系,若已知A(0,2),B(4,3),请求出相应的P点坐标。
