调查某初中1000名学生的肥胖情况,得下表:
| |
偏瘦 |
正常 |
肥胖 |
| 女生(人) |
100 |
173 |
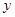 |
| 男生(人) |
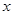 |
177 |
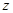 |
已知从这批学生中随机抽取1名学生,抽到偏瘦男生的概率为0.15。
(1)求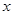 的值;
的值;
(2)若用分层抽样的方法,从这批学生中随机抽取50名,问应在肥胖学生中抽多少名?
(3)已知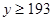 ,
,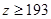 ,肥胖学生中男生不少于女生的概率。
,肥胖学生中男生不少于女生的概率。
相关知识点
推荐套卷
 中,直线
中,直线 的参数方程为
的参数方程为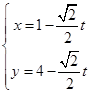 (t为参数),再以原点为极点,以x正半轴为极轴建立坐标系,并使得它与直角坐标系有相同的长度单位,在该极坐标系中圆C的方程为
(t为参数),再以原点为极点,以x正半轴为极轴建立坐标系,并使得它与直角坐标系有相同的长度单位,在该极坐标系中圆C的方程为 .
.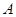 、
、 ,若点
,若点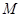 的坐标为
的坐标为 ,求
,求 的值.
的值.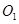 与圆
与圆 内切于点
内切于点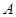 ,其半径分别为3与2,圆
,其半径分别为3与2,圆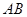 交圆
交圆 (
(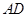 是圆
是圆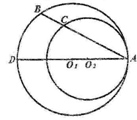
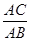 的值;
的值;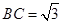 ,求
,求 和
和 使得
使得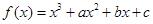
 .
. ,求
,求 的值;
的值;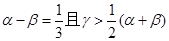 时,若存在实数
时,若存在实数 使得
使得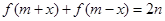 对任意
对任意 恒成立,求
恒成立,求 的最值.
的最值. 被圆
被圆 截得的弦长恰与椭圆
截得的弦长恰与椭圆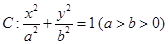 的短轴长相等,椭圆
的短轴长相等,椭圆 的离心率
的离心率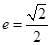 .
. 的动直线
的动直线 交椭圆
交椭圆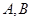 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点 ,使得无论
,使得无论 为直径的圆恒过定点
为直径的圆恒过定点


 2
2 为空气质量达到一级的天数,求
为空气质量达到一级的天数,求 为这一年中空气质量达到一级的天数,求
为这一年中空气质量达到一级的天数,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号