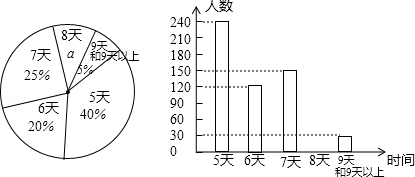
某校为积极开展人防教育，抽取了部分八年级的学生举行人防知识竞赛，并将竞赛成绩整理后作出如下的统计图。已知从左至右第一、二组的频率和是0.12，第二、三、四组的频数比是4：17：15，成绩不小于100分的同学占96%。结合统计图回答下列问题：从左至右第一组的频率是多少？共有多少人参加了这次人防知识竞赛？
成绩不小于130分的为优秀，若将原统计图改成扇形统计图，则优秀部分对应的圆心角应画成几度角？
如果这次竞赛成绩的中位数是120分，
那么成绩为120分的学生至少有多少人？
山地自行车越来越受到中学生的喜爱，各种品牌相继投放市场，某车行经营的A型车去年销售总额为5万元，今年每辆销售价比去年降低400元，若卖出的数量相同，销售总额将比去年减少20%．
（1）今年A型车每辆售价多少元？（用列方程的方法解答）
（2）该车计划新进一批A型车和新款B型车共60辆，且B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最多？
A，B两种型号车的进货和销售价格如下表：
如图，直线y=mx与双曲线y=
相交于A、B两点，A点的坐标为（1，2）
（1）求反比例函数的表达式
（2）根据图象直接写出当mx＞时，x的取值范围；
（3）计算线段AB的长．
区教育局为了解我区八年级学生参加社会实践活动情况，随机抽查了某校部分八年级学生第一学期参加社会实践活动的天数，并用得到的数据检测了两幅统计图，下面给出了两幅不完整的统计图（如图）
请根据图中提供的信息，回答下列问题：
（1）a=%，并写出该扇形所对圆心角的度数为，请补全条形图．
（2）在这次抽样调查中，众数和中位数分别是多少？
（3）如果该校共有八年级学生2000人，请你估计“活动时间不少于7天”的学生人数大约有多少人？
如图，AB是⊙O的直径，OD垂直于弦AC于点E，且交⊙O于点D，F是BA延长线上一点，若∠CDB=BFD．
（1）求证：FD是⊙O的一条切线；
（2）若AB=10，AC=8，求DF的长．
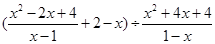，其中x满足x2﹣4x+3=0．
粤公网安备 44130202000953号