如图,已知直线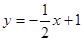 交坐标轴于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线另一个交点为E.
交坐标轴于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线另一个交点为E.
请直接写出点C,D的坐标;
求抛物线的解析式
若正方形以每秒
 个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围
个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围在(3)的条件下,抛物线与正方形一起平移,同时D落在x轴上时停止,求抛物线上C,E两点间的抛物线弧所扫过的面积.
相关知识点
推荐套卷

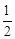 .
.

 km的C处.
km的C处.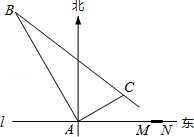
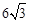 cm.
cm.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号