有一个数学活动,其具体操作过程是:
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开
(如图1);
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2).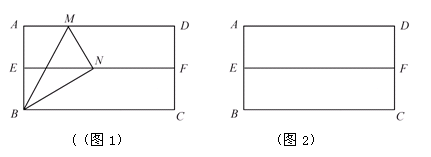
请解答以下问题:如图2,若延长MN交线段BC于P,△BMP是什么三角形?请证明你的结论.
在图2中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP
相关知识点
推荐套卷


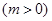 与x轴交于A ,B两点,且点A在点B的左侧,与y轴交于点C。
与x轴交于A ,B两点,且点A在点B的左侧,与y轴交于点C。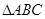 为等腰三角形时,求m的值;
为等腰三角形时,求m的值; 与点Q
与点Q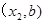 在(1)中抛物线上,
在(1)中抛物线上,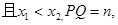 求
求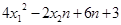 的值.
的值. (件)与销售单价
(件)与销售单价 (元)符合一次函数
(元)符合一次函数 ,且
,且 时,
时, ;
; 时,
时, .
. 元,试写出利润
元,试写出利润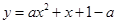 (a为常数)
(a为常数)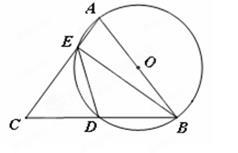
 粤公网安备 44130202000953号
粤公网安备 44130202000953号