(本题12分)南水北调工程中线已经在12月27日开始向北京、天津等地供水.为了进一步加强居民的节水意识,合理调配水资源,某区决定对本区的居民用水实行额定用水管理。为了更好的确定额定用水的用水量,首先对本区居民的目前生活用水量进行了入户调查.下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨).
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
(1)请你将调查数据进行如下整理:频数分布表
(2)结合整理的数据完成频数分布直方图,通过观察直方图你可以得到哪些信息?请你写出你得到的信息.

(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定多少吨?
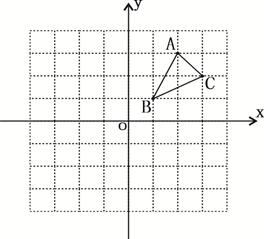
(1)将△ABC向下平移4个单位长度,画出平移后的△A1B1C1;
(2)画出△ABC关于y轴对称的△A2B2C2;.
(3)求出△ABC的面积.

(1)将△ABC向下平移4个单位长度,画出平移后的△A1B1C1;
(2)画出△ABC关于y轴对称的△A2B2C2;.
(3)求出△ABC的面积.