车站每天8∶00-9∶00,9∶00-10∶00都恰有一辆客车到站,8∶00-9∶00到站的客车A可能在8∶10,8∶30,8∶50到站,其概率依次为 ;9∶00-10∶00到站的客车B可能在9∶10,9∶30,9∶50到站,其概率依次为
;9∶00-10∶00到站的客车B可能在9∶10,9∶30,9∶50到站,其概率依次为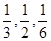 .
.
(1)旅客甲8∶00到站,设他的候车时间为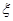 ,求
,求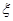 的分布列和
的分布列和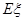 ;
;
(2)旅客乙8∶20到站,设他的候车时间为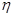 ,求
,求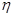 的分布列和
的分布列和 .
.
推荐套卷
车站每天8∶00-9∶00,9∶00-10∶00都恰有一辆客车到站,8∶00-9∶00到站的客车A可能在8∶10,8∶30,8∶50到站,其概率依次为 ;9∶00-10∶00到站的客车B可能在9∶10,9∶30,9∶50到站,其概率依次为
;9∶00-10∶00到站的客车B可能在9∶10,9∶30,9∶50到站,其概率依次为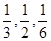 .
.
(1)旅客甲8∶00到站,设他的候车时间为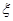 ,求
,求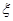 的分布列和
的分布列和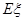 ;
;
(2)旅客乙8∶20到站,设他的候车时间为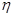 ,求
,求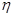 的分布列和
的分布列和 .
.