经市场调查，某种商品在120天内的日销售量和售价均为时间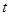
（天）的函数，日销售量与时间的关系用图（1）的一条折线表示，售价与时间的关系用图（2）的一条折线表示。
（Ⅰ）写出图（1）表示的日销售量（千克）与时间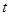的函数关系史
；
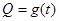写出图（2）表示的售价（元 /千克）与时间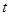的函数关系式
；
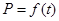（Ⅱ）求日销售额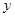
（元）与时间的函数关系式，并求出日销售额最高的是哪一天？最高的销售额是多少？（注：日销售额＝日销售量×售价）
相关试题
，圆
：
与
轴正半轴的交点为
，与曲线
的交点为
，直线
与
轴的交点为
.
表示
和
；
满足：
.
的值使数列
成等比数列；
的大小.
,函数
.
的单调区间和极值;
和
是函数
的值并证明:
.
，圆
，圆
,
关于直线
对称.
，使
点的距离减去
点的距离的差为
，如果存在求出
中，
底面
，
，
，
为
的中点，
为
的中点，点
在
上，且
.
平面
；
平面
；
的体积. 
和获得等级不是
、
、
，物理、化学、生物获得等级不是
、
、
.
）；
，并说明理由.推荐套卷
经市场调查，某种商品在120天内的日销售量和售价均为时间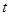（天）的函数，日销售量与时间的关系用图（1）的一条折线表示，售价与时间的关系用图（2）的一条折线表示。
（Ⅰ）写出图（1）表示的日销售量（千克）与时间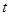的函数关系史；
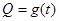写出图（2）表示的售价（元 /千克）与时间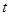的函数关系式；
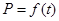（Ⅱ）求日销售额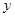（元）与时间的函数关系式，并求出日销售额最高的是哪一天？最高的销售额是多少？（注：日销售额＝日销售量×售价）
粤公网安备 44130202000953号