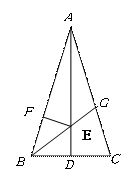
如图,在等腰三角形
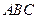 中,
中,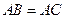 ,
,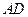 是
是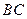 边上的中线,
边上的中线,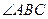 的平分线
的平分线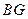 ,交
,交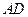 于点
于点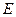 ,
,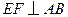 ,垂足为
,垂足为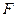 .
.
(1)若∠BAD = 20°,则∠C = .
(2)求证: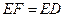 .
.
如图,
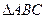 中,
中,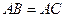 ,
,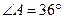 ,
,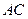 的垂直平分线交
的垂直平分线交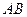 于
于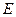 ,
,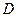 为垂足,连结
为垂足,连结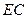 .
.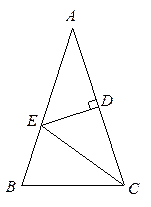
(1)求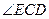 的度数;
的度数;
(2)若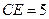 ,求
,求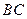 长
长
相关知识点
推荐套卷
如图,在等腰三角形
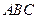 中,
中,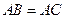 ,
,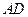 是
是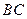 边上的中线,
边上的中线,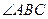 的平分线
的平分线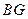 ,交
,交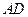 于点
于点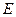 ,
,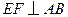 ,垂足为
,垂足为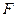 .
.
(1)若∠BAD = 20°,则∠C = .
(2)求证: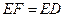 .
.
如图,
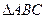 中,
中,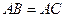 ,
,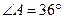 ,
,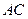 的垂直平分线交
的垂直平分线交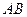 于
于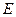 ,
,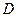 为垂足,连结
为垂足,连结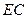 .
.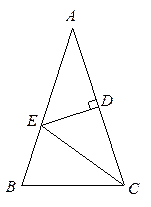
(1)求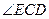 的度数;
的度数;
(2)若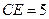 ,求
,求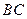 长
长