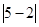 表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离;
表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离; 可以看做
可以看做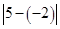 ,表示5与-2的差的绝对值,也可理解为5与-2两数在数轴上所对应的两点之间的距离.
,表示5与-2的差的绝对值,也可理解为5与-2两数在数轴上所对应的两点之间的距离.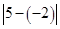 =___________.
=___________.
利用数轴,找出所有符合条件的整数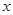 ,使
,使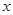 所表示的点到5和—2的距离之和为7
所表示的点到5和—2的距离之和为7
由以上探索猜想,对于任何有理数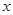 ,
,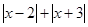 是否有最小值? 如果有,写出最
是否有最小值? 如果有,写出最
小值;如果没有,说明理由
相关知识点
推荐套卷
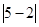 表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离;
表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离; 可以看做
可以看做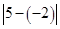 ,表示5与-2的差的绝对值,也可理解为5与-2两数在数轴上所对应的两点之间的距离.
,表示5与-2的差的绝对值,也可理解为5与-2两数在数轴上所对应的两点之间的距离.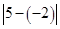 =___________.
=___________.
利用数轴,找出所有符合条件的整数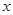 ,使
,使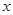 所表示的点到5和—2的距离之和为7
所表示的点到5和—2的距离之和为7
由以上探索猜想,对于任何有理数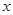 ,
,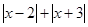 是否有最小值? 如果有,写出最
是否有最小值? 如果有,写出最
小值;如果没有,说明理由