(本小题12分)一个盒子中装有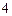 张卡片,每张卡片上写有
张卡片,每张卡片上写有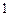 个数字,数字分别是
个数字,数字分别是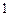 、
、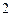 、
、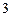 、
、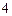 。现从盒子中随机抽取卡片,
。现从盒子中随机抽取卡片,
⑴若一次抽取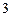 张卡片,求
张卡片,求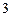 张卡片上数字之和大于
张卡片上数字之和大于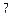 的概率;
的概率;
⑵若第一次抽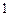 张卡片,放回后再抽取
张卡片,放回后再抽取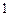 张卡片,求两次抽取中至少一次抽到数字
张卡片,求两次抽取中至少一次抽到数字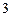 的概率。
的概率。
推荐套卷
(本小题12分)一个盒子中装有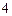 张卡片,每张卡片上写有
张卡片,每张卡片上写有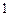 个数字,数字分别是
个数字,数字分别是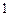 、
、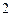 、
、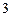 、
、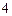 。现从盒子中随机抽取卡片,
。现从盒子中随机抽取卡片,
⑴若一次抽取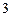 张卡片,求
张卡片,求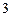 张卡片上数字之和大于
张卡片上数字之和大于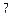 的概率;
的概率;
⑵若第一次抽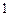 张卡片,放回后再抽取
张卡片,放回后再抽取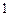 张卡片,求两次抽取中至少一次抽到数字
张卡片,求两次抽取中至少一次抽到数字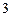 的概率。
的概率。