.数列 的各项均为正数,
的各项均为正数,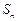 为其前
为其前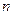 项和,对于任意
项和,对于任意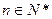 ,总有
,总有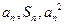 成等差数列.(Ⅰ)求数列
成等差数列.(Ⅰ)求数列 的通项公式;(Ⅱ)设数列
的通项公式;(Ⅱ)设数列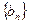 的前
的前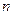 项和为
项和为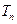 ,且
,且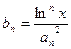 ,求证:对任意实数
,求证:对任意实数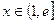 (
(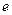 是常数,
是常数,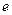 =2.71828
=2.71828 )和任意正整数
)和任意正整数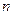 ,总有
,总有
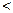 2;(Ⅲ) 正数数列
2;(Ⅲ) 正数数列 中,
中,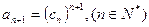 .求数列
.求数列 中的最大项.
中的最大项.
推荐套卷
.数列 的各项均为正数,
的各项均为正数,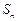 为其前
为其前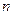 项和,对于任意
项和,对于任意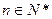 ,总有
,总有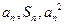 成等差数列.(Ⅰ)求数列
成等差数列.(Ⅰ)求数列 的通项公式;(Ⅱ)设数列
的通项公式;(Ⅱ)设数列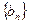 的前
的前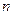 项和为
项和为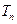 ,且
,且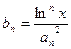 ,求证:对任意实数
,求证:对任意实数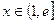 (
(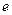 是常数,
是常数,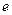 =2.71828
=2.71828 )和任意正整数
)和任意正整数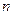 ,总有
,总有
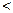 2;(Ⅲ) 正数数列
2;(Ⅲ) 正数数列 中,
中,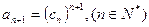 .求数列
.求数列 中的最大项.
中的最大项.