（本小题满分13分）如图，在三棱柱ABC—A1B1C1中，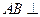
侧面BB1C1C，已知AB=BC=1，BB1=2，
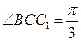，E为CC1的中点。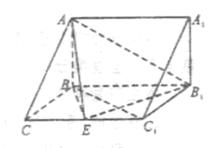
（1）求证：
平面ABC；
（2）求二面角A—B1E—B的大小。
中，角
、
、
对的边分别为
、
、
，且
，
.
的值；
，求
.
，
，
的解析式，并求它的单调递增区间；
有四个不相等的实数根，求
的取值范围。
。
的最小正周期和单调递增区间；
上的最小值和最大值，并求出取最值时
的值。
，求它的定义域和值域。
，计算：
；
．相关知识点
推荐套卷
（本小题满分13分）如图，在三棱柱ABC—A1B1C1中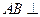，侧面BB1C1C，已知AB=BC=1，BB1=2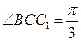，，E为CC1的中点。
（1）求证：平面ABC；
（2）求二面角A—B1E—B的大小。
粤公网安备 44130202000953号