（本小题满分12分）下表是种产品销售收入与销售量之间的一组数据：
| 销售量x(吨) |
2 |
3 |
5 |
6 |
| 销售收入y(千元) |
7 |
8 |
9 |
12 |
（I） 画出散点图；
（II） 求出回归方程；
（III） 根据回归方程估计销售量为9吨时的销售收入。
（参考数据：2×7+3×8+5×9+6×12=155，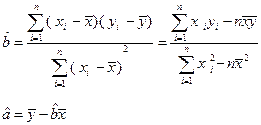
)
推荐套卷
（本小题满分12分）下表是种产品销售收入与销售量之间的一组数据：
| 销售量x(吨) |
2 |
3 |
5 |
6 |
| 销售收入y(千元) |
7 |
8 |
9 |
12 |
（I） 画出散点图；
（II） 求出回归方程；
（III） 根据回归方程估计销售量为9吨时的销售收入。
（参考数据：2×7+3×8+5×9+6×12=155，)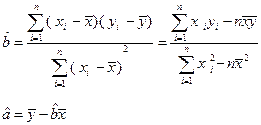
粤公网安备 44130202000953号