(本小题满分13分.其中(Ⅰ)小问6分,(Ⅱ)小问7分)
QQ先生的鱼缸中有7条鱼,其中6条青鱼和1条黑鱼,计划从当天开始,每天中午从该鱼缸中抓出1条鱼(每条鱼被抓到的概率相同)并吃掉.若黑鱼未被抓出,则它每晚要吃掉1条青鱼(规定青鱼不吃鱼).
(Ⅰ)求这7条鱼中至少有6条被QQ先生吃掉的概率;
(Ⅱ)以 表示这7条鱼中被QQ先生吃掉的鱼的条数,求
表示这7条鱼中被QQ先生吃掉的鱼的条数,求 的分布列及其数学期望
的分布列及其数学期望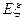 .
.
推荐套卷
(本小题满分13分.其中(Ⅰ)小问6分,(Ⅱ)小问7分)
QQ先生的鱼缸中有7条鱼,其中6条青鱼和1条黑鱼,计划从当天开始,每天中午从该鱼缸中抓出1条鱼(每条鱼被抓到的概率相同)并吃掉.若黑鱼未被抓出,则它每晚要吃掉1条青鱼(规定青鱼不吃鱼).
(Ⅰ)求这7条鱼中至少有6条被QQ先生吃掉的概率;
(Ⅱ)以 表示这7条鱼中被QQ先生吃掉的鱼的条数,求
表示这7条鱼中被QQ先生吃掉的鱼的条数,求 的分布列及其数学期望
的分布列及其数学期望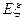 .
.