如图，在平面直角坐标系中，△ ABC的三个顶点的坐标分别为A（0,1），B（-1,1），C（-1,3）。画出△ABC关于x轴对称的△A1B1C1，并写出点C1的坐标；
画出△ABC绕原点O顺时针方向旋转90°后得到的△A2B2C2，并写出点C2的坐标；，
将△A2B2C2平移得到△ A3B3C3，使点A2的对应点是A3，点B2的对应点是B3，点C2的对应点是C3（4，-1），在坐标系中画出△ A3B3C3，并写出点A3，B3的坐标。
相关试题
．如图，已知A、B两点的坐标分别为A（0，2
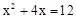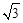），B（2，0）直线AB与反比例函数
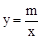的图象交与点C和点D（－1，a）．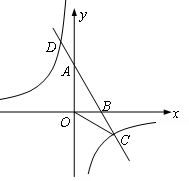
（1）求直线AB和反比例函数的解析式；
（2）求∠ACO的度数．
如图，矩形ABCD的对角线相交于点O，DE∥CA，AE∥BD．
（1）求证：四边形AODE是菱形；
（2）若将题设中“矩形ABCD”这一条件改为“菱形ABCD”，其余条件不变，则四边形AODE的形状是什么？说明理由．
如图所示，制作一种产品的同时，需将原材料加热，设该材料温度为y℃，从加热开始计算的时间为x分钟．据了解，该材料在加热过程中温度y与时间x成一次函数关系，已知该材料在加热前的温度为l5℃，加热5分钟使材料温度达到60℃时停止加热，停止加热后，材料温度逐渐下降，这时温度y与时间x成反比例函数关系．
（1）分别求出该材料加热和停止加热过程中y与x的函数关系（要写出x的取值范围）；
（2）根据工艺要求，在材料温度不低于30℃的这段时间内，需要对该材料进行特殊处理，那么对该材料进行特殊处理所用的时间为多少分钟？
相关知识点
推荐套卷
粤公网安备 44130202000953号