如图，某兴趣小组测得菱形养殖区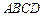
的固定投食点
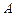到两条平行河岸线
的距离分别为4m、8m，河岸线
与该养殖区的最近点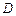
的距离为1m，
与该养殖区的最近点
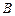的距离为2m．
（1）如图甲，养殖区在投食点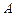的右侧，若该小组测得
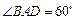，请据此算出养殖区的面积；
（2）如图乙，养殖区在投食点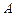的两侧，试在该小组未测得
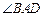的大小的情况下，估算出养殖区的最小面积．
是以
为焦点的椭圆上一点，且
，求证：椭圆的离心率为
.
，使方程
的两个根是一个直角三角形的两个锐角的正弦值.
，
，
.求
的值.
中，已知
，求
的值.
，求证：
.推荐套卷
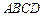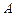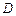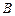如图，某兴趣小组测得菱形养殖区的固定投食点到两条平行河岸线的距离分别为4m、8m，河岸线与该养殖区的最近点的距离为1m，与该养殖区的最近点的距离为2m．
（1）如图甲，养殖区在投食点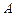的右侧，若该小组测得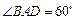，请据此算出养殖区的面积；
（2）如图乙，养殖区在投食点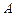的两侧，试在该小组未测得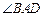的大小的情况下，估算出养殖区的最小面积．
粤公网安备 44130202000953号