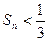（本小题满分14分）已知曲线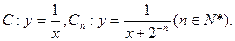
从C上一点Qn（xn，yn）作x轴的垂线，交Cn于点Pn，再从点Pn作y轴的垂线，交C于点Qn+1（xn+1，yn+1）。设x1＝1，an＝xn+1－xn，bn＝yn－yn+1
①求Q1，Q2的坐标 ；②求数列{an}的通项公式；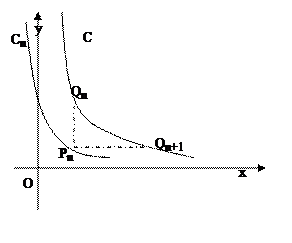
③记数列{an·bn}的前n项和为Sn，求证：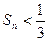
推荐套卷
（本小题满分14分）已知曲线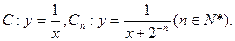从C上一点Qn（xn，yn）作x轴的垂线，交Cn于点Pn，再从点Pn作y轴的垂线，交C于点Qn+1（xn+1，yn+1）。设x1＝1，an＝xn+1－xn，bn＝yn－yn+1
①求Q1，Q2的坐标 ；②求数列{an}的通项公式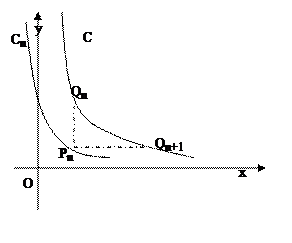；③记数列{an·bn}的前n项和为Sn，求证：
粤公网安备 44130202000953号