(共8分)对于有理数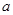 、
、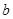 ,定义运算:“
,定义运算:“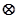 ”,
”,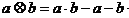
(1)计算:3
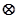 (-5)的值;
(-5)的值;(2)填空:
 (填“>”或“=”或“<”);我们知道:有理数的加法运算和乘法运算满足交换律.那么,由以上计算的结果进行猜想:“
(填“>”或“=”或“<”);我们知道:有理数的加法运算和乘法运算满足交换律.那么,由以上计算的结果进行猜想:“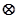 ” 交换律。(填“满足”或“不满足”)
” 交换律。(填“满足”或“不满足”)(3)如果(x-2)
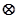 3=3,求x的值。
3=3,求x的值。
相关知识点
推荐套卷
(共8分)对于有理数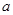 、
、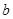 ,定义运算:“
,定义运算:“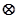 ”,
”,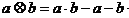
(1)计算:3
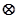 (-5)的值;
(-5)的值;(2)填空:
 (填“>”或“=”或“<”);我们知道:有理数的加法运算和乘法运算满足交换律.那么,由以上计算的结果进行猜想:“
(填“>”或“=”或“<”);我们知道:有理数的加法运算和乘法运算满足交换律.那么,由以上计算的结果进行猜想:“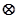 ” 交换律。(填“满足”或“不满足”)
” 交换律。(填“满足”或“不满足”)(3)如果(x-2)
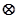 3=3,求x的值。
3=3,求x的值。