(本小题满分14分)
已知函数 是奇函数,且满足
是奇函数,且满足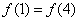
(Ⅰ)求实数 、
、 的值;
的值;
(Ⅱ)试证明函数 在区间
在区间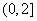 单调递减,在区间
单调递减,在区间 单调递增;
单调递增;
(Ⅲ)是否存在实数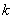 同时满足以下两个条件:①不等式
同时满足以下两个条件:①不等式 对
对 恒成立;
恒成立;
②方程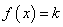 在
在 上有解.若存在,试求出实数
上有解.若存在,试求出实数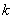 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
推荐套卷
(本小题满分14分)
已知函数 是奇函数,且满足
是奇函数,且满足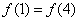
(Ⅰ)求实数 、
、 的值;
的值;
(Ⅱ)试证明函数 在区间
在区间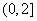 单调递减,在区间
单调递减,在区间 单调递增;
单调递增;
(Ⅲ)是否存在实数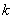 同时满足以下两个条件:①不等式
同时满足以下两个条件:①不等式 对
对 恒成立;
恒成立;
②方程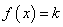 在
在 上有解.若存在,试求出实数
上有解.若存在,试求出实数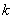 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.