平面内有一等腰直角三角板（∠ACB=90°）和一直线MN.过点C作CE⊥MN于点E,过点B作BF⊥MN于点F.当点E与点A重合时（如图1）,易证:AF+BF=2CE.当三角板绕点A顺时针旋转至图2、图3的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.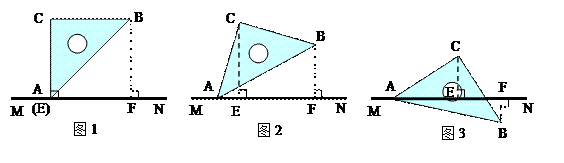
是同类项，求m，n.
的值.
时，求代数式(2m-3n)(m+n)+
的值.相关知识点
推荐套卷
平面内有一等腰直角三角板（∠ACB=90°）和一直线MN.过点C作CE⊥MN于点E,过点B作BF⊥MN于点F.当点E与点A重合时（如图1）,易证:AF+BF=2CE.当三角板绕点A顺时针旋转至图2、图3的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.
粤公网安备 44130202000953号