如图,在△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:①AD=CB,②AE=CF,③∠B=∠D,④AD∥BC.请用其中三个作为已知条件,余下一个作为求证结论,编一道数学问题,并写出解答过程:
已知条件: , , ;
求证结论: .
证明: 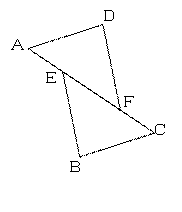
相关知识点
推荐套卷
如图,在△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:①AD=CB,②AE=CF,③∠B=∠D,④AD∥BC.请用其中三个作为已知条件,余下一个作为求证结论,编一道数学问题,并写出解答过程:
已知条件: , , ;
求证结论: .
证明: 