如图，在四面体ABOC中，OC⊥OA，OC⊥OB，∠AOB＝120°，且OA＝OB＝OC＝1.
(1)设P为AC的中点．证明：在AB上存在一点Q，使PQ⊥OA，并计算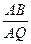
的值；
(2)求二面角O－AC－B的平面角的余弦值．
相关试题
与直线
：
交于
两点,
为坐标原点.
过椭圆的左焦点，且
，求
的面积；
，且直线
相切，求圆
的半径
的值．
．
时，求
的值域；
的内角
的对边分别为
，且满足
，
，求
的值．
满足
的前
项和
．
和直线
．
总有两个不同的交点
；
中点
的轨迹方程，并说明其轨迹是什么曲线？
，
是
的导函数，则函数
的最大值是相关知识点
推荐套卷
如图，在四面体ABOC中，OC⊥OA，OC⊥OB，∠AOB＝120°，且OA＝OB＝OC＝1.
(1)设P为AC的中点．证明：在AB上存在一点Q，使PQ⊥OA，并计算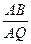的值；
(2)求二面角O－AC－B的平面角的余弦值．
粤公网安备 44130202000953号