(本题满分16分)设函数y=f(x)对任意实数x，都有f(x)=2f(x+1)，当x∈[0,1]时，f(x)=
x2(1-x).
(Ⅰ)已知n∈N+，当x∈[n,n+1]时，求y=f(x)的解析式；
(Ⅱ)求证：对于任意的n∈N+，当x∈[n,n+1]时，都有|f(x)|≤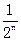
；
(Ⅲ)对于函数y=f(x)
(x∈[0,+∞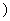
，若在它的图象上存在点P，使经过点P的切线与直线x+y=1平行，那么这样点有多少个？并说明理由
相关试题
中，
，
． 
的值；
，求
（ω＞0）
）上是增函数，求ω最大值
的最小正周期、最大值、最小值
最小正周期为π，最大值为3，且
≠0），求f (x)的的解析式。推荐套卷
(本题满分16分)设函数y=f(x)对任意实数x，都有f(x)=2f(x+1)，当x∈[0,1]时，f(x)=x2(1-x).
(Ⅰ)已知n∈N+，当x∈[n,n+1]时，求y=f(x)的解析式；
(Ⅱ)求证：对于任意的n∈N+，当x∈[n,n+1]时，都有|f(x)|≤；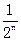
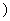(Ⅲ)对于函数y=f(x)(x∈[0,+∞，若在它的图象上存在点P，使经过点P的切线与直线x+y=1平行，那么这样点有多少个？并说明理由
粤公网安备 44130202000953号