如图,在△ABC中,分别以AB,AC为直径在△ABC外作半圆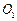 和半圆
和半圆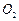 ,其中
,其中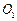 和
和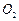 分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点.
分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点. 
(1)连结 ,
,
证明: ;
;
(2)如图,过点A分别作半圆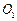 和半圆
和半圆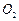 的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;
的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;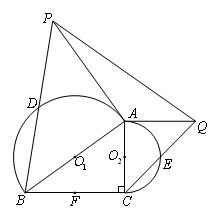
(3)如图三,过点A作半圆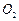 的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆
的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆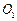 的切线.
的切线.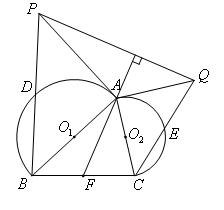
相关知识点
推荐套卷
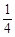 ,求这个角.
,求这个角.
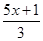 -
-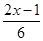 =1.
=1.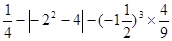 ;
;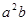

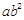 )
)

 粤公网安备 44130202000953号
粤公网安备 44130202000953号