(满分l0分)如图，△ABC是等边三角形，点D是AC的中点，延长BC到点E，使CE=CD．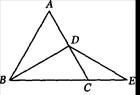
(1)用尺规作图的方法，过点D作DM⊥BE，垂足为M(不写作法，保留作图痕迹)；
(2)求证：BM=EM．
相关知识点
推荐套卷
(满分l0分)如图，△ABC是等边三角形，点D是AC的中点，延长BC到点E，使CE=CD．
(1)用尺规作图的方法，过点D作DM⊥BE，垂足为M(不写作法，保留作图痕迹)；
(2)求证：BM=EM．
粤公网安备 44130202000953号