（本小题满分8分）甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地，乙车比甲车晚出发2小时（从甲车出发时开始计时）．图中折线
、线段
分别表示甲、乙两车所行路程
（千米）与时间
（小时）之间的函数关系对应的图象（线段
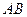表示甲出发不足2小时因故停车检修）．请根据图象所提供的信息，解决如下问题：
（1）求乙车所行路程与时间的函数关系式；
（2）求两车在途中第二次相遇时，它们距出发地的路程；
（3）乙车出发多长时间，两车在途中第一次相遇？（写出解题过程）
相关试题
已知：如图，抛物线 经过原点 和点 ， 为抛物线上的一个动点，过点 作 轴的垂线，垂足为 ，并与直线 交于点 ．
（1）求抛物线的解析式；
（2）当点 在直线 上方时，求线段 的最大值；
（3）过点 作 轴于点 ，在抛物线上是否存在点 ，使得以 、 、 、 四点为顶点的四边形是平行四边形？若存在，求 的值；若不存在，请说明理由．
相关知识点
推荐套卷
粤公网安备 44130202000953号