如图所示，某居民楼Ⅰ高20米，窗户朝南。该楼内一楼住户的窗台离地面距离CM为2米，窗户CD高1.8米。现计划在I楼的正南方距I楼30米处新建一居民楼Ⅱ。当正午时刻太阳光线与地面成30°角时，要使Ⅱ楼的影子不影响I楼所有住户的采光，新建Ⅱ楼最高只能盖多少米?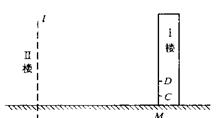
÷
，其中x＝
＋1.
÷
，其中x满足x2－x－1＝0.
＋1，y＝
的值．相关知识点
推荐套卷
如图所示，某居民楼Ⅰ高20米，窗户朝南。该楼内一楼住户的窗台离地面距离CM为2米，窗户CD高1.8米。现计划在I楼的正南方距I楼30米处新建一居民楼Ⅱ。当正午时刻太阳光线与地面成30°角时，要使Ⅱ楼的影子不影响I楼所有住户的采光，新建Ⅱ楼最高只能盖多少米?
粤公网安备 44130202000953号