（本小题满分10分）一名学生在军训中练习射击项目，他射击一次，命中目标的概率是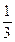
，若连续射击6次，且各次射击是否命中目标相互之间没有影响．
（1）求这名学生在第3次射击时，首次命中目标的概率；
（2）求这名学生在射击过程中，恰好命中目标3次的概率．
中，
，
，
. 以
点
为圆心，线段
的长为半径的半圆分别交
所在直线于点
、
，交线段
于点
，求弧
的长.（精确到
）
，且以下命题都为真命题：
实系数一元二次方程
的两根都是虚数；
存在复数
同时满足
且
.
的取值范围.
.
；
.相关知识点
推荐套卷
（本小题满分10分）一名学生在军训中练习射击项目，他射击一次，命中目标的概率是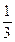，若连续射击6次，且各次射击是否命中目标相互之间没有影响．
（1）求这名学生在第3次射击时，首次命中目标的概率；
（2）求这名学生在射击过程中，恰好命中目标3次的概率．
粤公网安备 44130202000953号