已知△DCE的顶点C在ÐAOB的平分线OP上,CD交OA于F, CE交OB于G.

(1)如图1,若CD^ OA, CE^OB, 则图中有哪些相等的线段, 请直接写出你的结论:
;
(2)如图2, 若ÐAOB=120°, ÐDCE =ÐAOC, 试判断线段CF与线段CG的数量关系并
加以证明;
(3)若ÐAOB=a,当ÐDCE满足什么条件时,你在(2)中得到的结论仍然成立, 请
直接写出ÐDCE满足的条件.
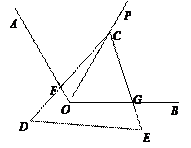
相关知识点
推荐套卷
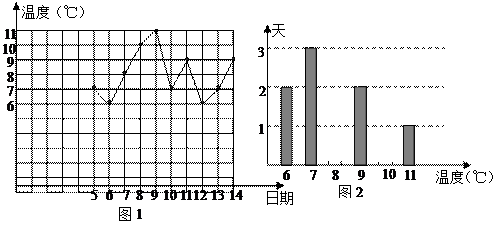
 造成巨大的经济损失.我市某学校学生积极捐款支援灾区,该校初二(1)班45名同学共捐款2300元,捐款情况如下表.表中捐款20元和50元的人数不小心被墨水污染已看不清楚,请你帮助确定表中数据,并说明理由.
造成巨大的经济损失.我市某学校学生积极捐款支援灾区,该校初二(1)班45名同学共捐款2300元,捐款情况如下表.表中捐款20元和50元的人数不小心被墨水污染已看不清楚,请你帮助确定表中数据,并说明理由. 中,
中, ,
, ,点
,点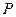 是边
是边 上的动点(点
上的动点(点 ,点
,点 重合),过点
重合),过点 ,交
,交 边于
边于 点,再把
点,再把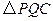 沿着动直线
沿着动直线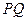 对折,点
对折,点 点,设
点,设 的长度为
的长度为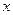 ,
,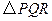 与矩形
与矩形 .
. 的度数;
的度数; 边上?
边上? ?
?
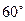 .
.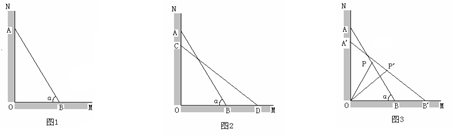 ②如图3,当A点下滑到A’点,B点向右滑行到B’点
②如图3,当A点下滑到A’点,B点向右滑行到B’点 时,梯子AB的中点P也随之运动到P’点.若∠POP’=
时,梯子AB的中点P也随之运动到P’点.若∠POP’=  ,求AA’的长和点P运动的路线长。
,求AA’的长和点P运动的路线长。 以加热的饮水机,该饮水机的工作程序是:放满水后,
以加热的饮水机,该饮水机的工作程序是:放满水后, 接通电源,则自动开始加热,每分钟水温上升10ºC,待加热到100ºC,饮水机自动切断电源,水温开始下降,水温和时间成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20ºC,接通电源后,水温和时间的关系下图所示,回答下列问题;
接通电源,则自动开始加热,每分钟水温上升10ºC,待加热到100ºC,饮水机自动切断电源,水温开始下降,水温和时间成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20ºC,接通电源后,水温和时间的关系下图所示,回答下列问题;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号