(本题12分)在梯形ABCD中,AB∥CD,∠BCD=90,且AB=1,BC=2,tan∠ADC=2;对角线相交于O点,等腰直角三角板的直角顶点落在梯形的顶点C上,使三角板绕点C旋转。
(1)当三角板旋转到图1的位置时,猜想DE与BF的数量关系,并加以证明。
(2)在(1)问条件下,若BE:CE=1:2,∠BEC=135°,求sin∠BFE的值。
(3)当三角板的一边CF与梯形对角线AC重合时,作DH⊥PE于H,如图2,若OF= 时,求PE及DH的长。
时,求PE及DH的长。
相关知识点
推荐套卷




 求证:∠B=∠E.
求证:∠B=∠E.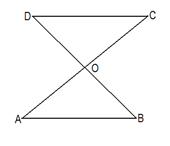
 粤公网安备 44130202000953号
粤公网安备 44130202000953号