已知函数
，且定义域为（0，2）.
（1）求关于x的方程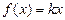
+3在（0，2）上的解；
（2）若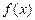
是定义域(0，2)上的单调函数，求实数
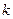的取值范围；
（3）若关于x的方程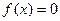
在（0，2）上有两个不同的解
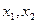，求k的取值范围。
相关试题
上一点M的纵坐标为2．
共焦点的椭圆方程．
恒成立，
方程
表示焦点在
轴上的椭圆，若命题“
且
”为假，求实数
的取值范围．
若非
是
的充分不必要条件，求
的取值范围．
的前
项和
，
的通项公式；
，求数列
的前
项和
．
中，
，
，
，点
是
的中点,
的值和中线
的长相关知识点
推荐套卷
已知函数，且定义域为（0，2）.
（1）求关于x的方程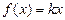+3在（0，2）上的解；
（2）若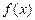是定义域(0，2)上的单调函数，求实数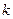的取值范围；
（3）若关于x的方程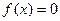在（0，2）上有两个不同的解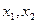，求k的取值范围。
粤公网安备 44130202000953号