(本题满分12分,(Ⅰ)小问3分,(Ⅱ)小问5分,(Ⅲ)小问4分.)
函数 的定义域为
的定义域为 ,并满足以下条件:①对任意
,并满足以下条件:①对任意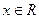 ,有
,有 ;②对任意
;②对任意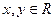 ,有
,有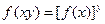 ;③
;③ .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求证: 在
在 上是单调增函数;
上是单调增函数;
(Ⅲ)若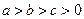 ,且
,且 ,求证:
,求证: .
.
推荐套卷
(本题满分12分,(Ⅰ)小问3分,(Ⅱ)小问5分,(Ⅲ)小问4分.)
函数 的定义域为
的定义域为 ,并满足以下条件:①对任意
,并满足以下条件:①对任意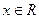 ,有
,有 ;②对任意
;②对任意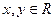 ,有
,有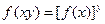 ;③
;③ .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求证: 在
在 上是单调增函数;
上是单调增函数;
(Ⅲ)若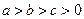 ,且
,且 ,求证:
,求证: .
.