某楼盘准备以每平方米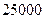 元的均价对外销售,由于国务院有关房地产的新政策出台,购房者持币观望.为了加快资金周转,房地产开发商对价格进行两次下调,最终以每平方米
元的均价对外销售,由于国务院有关房地产的新政策出台,购房者持币观望.为了加快资金周转,房地产开发商对价格进行两次下调,最终以每平方米 元的均价开盘销售.
元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)某人准备以每平方米 元的均价购买一套
元的均价购买一套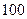 平方米的房子.开发商还给予以下两种优惠方案以供选择:①一次付清全款打九九折;②一次付清全款不打折,送五年物业管理费.如该楼盘物业管理费是每月
平方米的房子.开发商还给予以下两种优惠方案以供选择:①一次付清全款打九九折;②一次付清全款不打折,送五年物业管理费.如该楼盘物业管理费是每月 元/米2.请问哪种方案更优惠?
元/米2.请问哪种方案更优惠?
相关知识点
推荐套卷
某楼盘准备以每平方米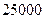 元的均价对外销售,由于国务院有关房地产的新政策出台,购房者持币观望.为了加快资金周转,房地产开发商对价格进行两次下调,最终以每平方米
元的均价对外销售,由于国务院有关房地产的新政策出台,购房者持币观望.为了加快资金周转,房地产开发商对价格进行两次下调,最终以每平方米 元的均价开盘销售.
元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)某人准备以每平方米 元的均价购买一套
元的均价购买一套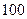 平方米的房子.开发商还给予以下两种优惠方案以供选择:①一次付清全款打九九折;②一次付清全款不打折,送五年物业管理费.如该楼盘物业管理费是每月
平方米的房子.开发商还给予以下两种优惠方案以供选择:①一次付清全款打九九折;②一次付清全款不打折,送五年物业管理费.如该楼盘物业管理费是每月 元/米2.请问哪种方案更优惠?
元/米2.请问哪种方案更优惠?