已知f (x)＝ax－ln(－x)，x∈(－e,0)，g(x)＝－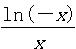
，其中e是自然常数，a∈R．
（1）讨论a＝－1时, f (
x)的单调性、极值；
（2）求证：在（1）的条件下，|f (x)|＞g(x)＋1/2；
（3）是否存在实数a，使f (x)的最小值是3，如果存在，求出a的值；如果不存在，说明理由．
，若球与正四面体的六条棱都相切，求这个正四面体外接球的体积。
，求这个正四面体外接球的体积。
，若球与正四面体的六条棱都相切，求这个正四面体外接球的表面积。
，求这个正四面体外接球的表面积。推荐套卷
已知f (x)＝ax－ln(－x)，x∈(－e,0)，g(x)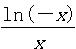＝－，其中e是自然常数，a∈R．
（1）讨论a＝－1时, f (x)的单调性、极值；
（2）求证：在（1）的条件下，|f (x)|＞g(x)＋1/2；
（3）是否存在实数a，使f (x)的最小值是3，如果存在，求出a的值；如果不存在，说明理由．
粤公网安备 44130202000953号