如图，现在要在一块半径为1m．圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ，使点P在AB弧上，点Q在OA上，点M,N在OB上，设∠BOP＝θ，YMNPQ的面积为S．
（1）求S关于θ的函数关系式；
（2）求S的最大值及相应θ的值
1. 
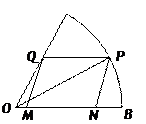
2.
甲（元）、
与圆C相切，且直线
距离的最大值与最小值
推荐套卷
如图，现在要在一块半径为1m．圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ，使点P在AB弧上，点Q在OA上，点M,N在OB上，设∠BOP＝θ，YMNPQ的面积为S．
（1）求S关于θ的函数关系式；
（2）求S的最大值及相应θ的值
1.
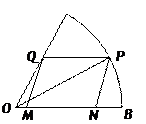
2.
粤公网安备 44130202000953号