（本题12分）
如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”．如：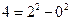
，
，
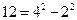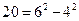，因此
，
，
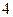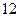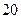这三个数都是神秘数．
（1）
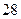和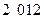
这两个数是神秘数吗？为什么？
（2）设两个连续偶数为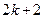
和
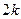（其中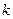
取非负整数），由这两个连续偶数构造的神秘数是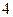的倍数吗？为什么？
（3）两个连续奇数的平方差（取正数）是神秘数吗？为什么？
（本题12分）
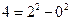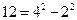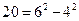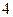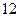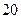如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”．如：，，，因此，，这三个数都是神秘数．
（1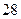）和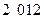这两个数是神秘数吗？为什么？
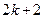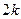（2）设两个连续偶数为和（其中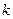取非负整数），由这两个连续偶数构造的神秘数是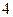的倍数吗？为什么？
（3）两个连续奇数的平方差（取正数）是神秘数吗？为什么？
ACB=
△BCD；
+DB
，然后选取一个使原式有意义的
的值代入求值.
—
)·
÷(
+
)
粤公网安备 44130202000953号