在湖南电视台举行的“快乐女声”比赛中，甲、乙、丙三位评委对选手的综合表现，分别给出“待定”或“通过”的结论．
(1).写出三位评委给出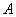
选手的所有可能的结论；
(2).对于选手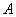，只有甲、乙两位评委给出相同结论的概率是多少？
相关试题
，
，点
在
轴上，
．
，求点
的坐标．
，并写出该不等式组的整数解．
，并把解集在数轴上表示出来．
相关知识点
推荐套卷
在湖南电视台举行的“快乐女声”比赛中，甲、乙、丙三位评委对选手的综合表现，分别给出“待定”或“通过”的结论．
(1).写出三位评委给出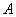选手的所有可能的结论；
(2).对于选手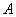，只有甲、乙两位评委给出相同结论的概率是多少？
粤公网安备 44130202000953号