某班组织春游,A、B两个风景点全班每人任选一处。去A风景点的每人付费25元,去B风景点的每人付费35元。若去B风景点的人数比去A风景点的少4人,全班共付费1660元。问全班有多少人?
解:设去A风景点的学生有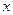 人,则全班有( )人,
人,则全班有( )人,
根据题意,得
解这个方程,得 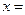
∴
答:全班有 人。
相关知识点
推荐套卷
某班组织春游,A、B两个风景点全班每人任选一处。去A风景点的每人付费25元,去B风景点的每人付费35元。若去B风景点的人数比去A风景点的少4人,全班共付费1660元。问全班有多少人?
解:设去A风景点的学生有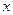 人,则全班有( )人,
人,则全班有( )人,
根据题意,得
解这个方程,得 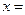
∴
答:全班有 人。