如图，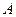
、
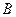两座城市相距100千米，现计划在这两座城市之间修筑一条高等级公路（即线段
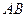）。经测量，森林保护区中心
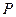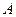点在城市的北偏东30°方向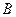，城市的北偏西45°方向上，已知森林保护区的范围在以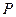为圆心，50千米为半径的圆形区域内。请问：计划修筑的这条高等级公路会不会穿越保护区，为什么？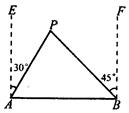
相关试题
少元？
经销乙种型号电脑．已知甲种电脑每台进价为3500元，乙种电脑每台进价为3000元，公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑
共15台，有几种进货方案？相关知识点
推荐套卷
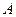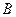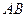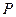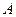如图，、两座城市相距100千米，现计划在这两座城市之间修筑一条高等级公路（即线段）。经测量，森林保护区中心点在城市的北偏东30°方向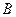，城市的北偏西45°方向上，已知森林保护区的范围在以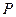为圆心，50千米为半径的圆形区域内。请问：计划修筑的这条高等级公路会不会穿越保护区，为什么？
粤公网安备 44130202000953号