小明和小刚用如图所示的两个转盘做游戏，游戏规则如下：分别旋转两个转盘，当两个转盘所转到的数字之积为奇数时，小明得2分；当所转到的数字之积为偶数时，小刚得1分。这个游戏对双方公平吗？若公平，说明理由。若不公平，如何修改规则才能使游戏对双方公平？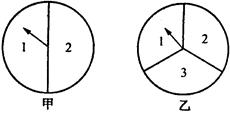
相关试题
”是新规定的这样一种运算法则：
，比如
(8分)
的值；
，求
的值；
＝
a2+8a-
-6a-
a2+
，其中a=
，其中 
）相关知识点
推荐套卷
小明和小刚用如图所示的两个转盘做游戏，游戏规则如下：分别旋转两个转盘，当两个转盘所转到的数字之积为奇数时，小明得2分；当所转到的数字之积为偶数时，小刚得1分。这个游戏对双方公平吗？若公平，说明理由。若不公平，如何修改规则才能使游戏对双方公平？
粤公网安备 44130202000953号