(理科)已知函数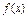 =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m.
(Ⅰ)若y=f(x)在[-1,1]上存在零点,求实数a的取值范围;
(Ⅱ)当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,求实数m的取值范围;
(Ⅲ)若函数y=f(x)(x∈[t,4])的值域为区间D,是否存在常数t,使区间D的长度为7-2t?若存在,求出t的值;若不存在,请说明理由(注:区间[p,q]的长度为q-p).
推荐套卷
(理科)已知函数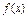 =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m.
(Ⅰ)若y=f(x)在[-1,1]上存在零点,求实数a的取值范围;
(Ⅱ)当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,求实数m的取值范围;
(Ⅲ)若函数y=f(x)(x∈[t,4])的值域为区间D,是否存在常数t,使区间D的长度为7-2t?若存在,求出t的值;若不存在,请说明理由(注:区间[p,q]的长度为q-p).