(本题12分)在正方形网格 中以点
中以点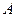 为圆心,
为圆心,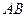 为半径作圆
为半径作圆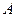 交网格于点
交网格于点 (如图(1)),过点
(如图(1)),过点 作圆的切线交网格于点
作圆的切线交网格于点 ,以点
,以点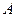 为圆心,
为圆心, 为半径作圆交网格于点
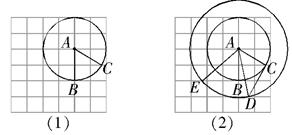
为半径作圆交网格于点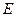
(如图(2)).
|
问题:
(1)求 的度数;
的度数;(2)求证:

 ;
;(3)
 可以看作是由
可以看作是由 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断 的形状(不用说明理由).
的形状(不用说明理由).(4)如图(
 3),已知直线
3),已知直线 ,且a∥b,b∥c,在图中用
,且a∥b,b∥c,在图中用 直尺、三角板、圆规画等边三角形
直尺、三角板、圆规画等边三角形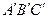 ,使三个顶点
,使三个顶点 ,分别在直线
,分别在直线 上.要求写出简要的画图过程,不需要说明理由.
上.要求写出简要的画图过程,不需要说明理由.
相关知识点
推荐套卷
 销售量】
销售量】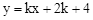 与抛物线
与抛物线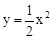 交于A、B两点,
交于A、B两点,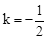 时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;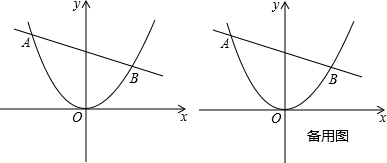
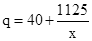 .
.
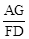 的值为 .
的值为 .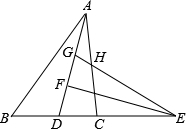
 粤公网安备 44130202000953号
粤公网安备 44130202000953号