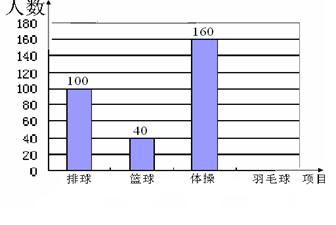
学校为了学生的身体健康，每天开展体育活动一小时，开设排球、篮球、羽毛
球、体操课．学生可根据自己的爱好任选其中一项，老师
根据学生报名情况进行了统计，并绘制了右边尚未完成的扇形统计图和频数分布直方图，请你结合图中的信息，解答下列问题：
（1）该校学生报名总人数有多少人？
（2）从表中可知选羽毛球的学生有多少人？选排球和篮球的人数分别占报名总人数的百分
之几？
（3）将两个统计图补充完整． 
相关试题
，求代数式
的值
(12分)如图，抛物线的顶点为A（2，1），且经过原点O，与x轴的另一个交点为B．
（1）求抛物线的解析式；
（2）在抛物线上求点M，使△MOB的面积是△AOB面积的3倍；
（3）连结OA，AB，在x轴下方的抛物线上是否存在点N，使△OBN与△OAB相似？若存在，求出N点的坐标；若不存在，说明理由．
的图象与反比例函数
的图象交于
两点，与
轴交于点
，与
轴交于点
，已知
，
，点
的坐标为
．
是半圆
的直径，弦
，
是
．判断直线
与半圆
册，6元的图书购买
册，求相关知识点
推荐套卷
粤公网安备 44130202000953号