梯形ABCD中,AD∥BC,BC=20cm,AD=10cm,现有两个动点P、Q分别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,线段PQ与BD相交于点E,过E作EF∥BC交CD于点F,射线QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0<t<10).
(1)当t为何值时,四边形PCDQ为平行四边形?
(2)在P、Q移动的过程中,线段PH的长是否发生改变?如果不变,求出线段PH的长;如果改变,请说明理由.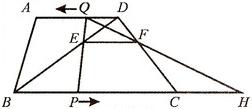
相关知识点
推荐套卷


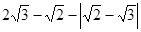 (2)
(2)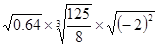
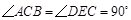 ,
,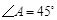 ,
,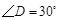 ,斜边
,斜边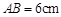 ,
, .把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点
.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点 、与D1E1相交于点F.
、与D1E1相交于点F.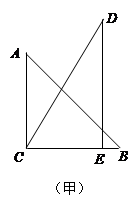
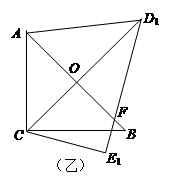
 的度数;
的度数; 顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由。
顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由。 粤公网安备 44130202000953号
粤公网安备 44130202000953号