(本小题14分)已知f(x)=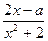 (x∈R)在区间[-1,1]上是增函数,
(x∈R)在区间[-1,1]上是增函数,
(1)求实数a的值组成的集合A;
(2)设关于x的方程f(x)= 的两个非零实根为x1、x2。试问:是否存在实数m,使得不等
的两个非零实根为x1、x2。试问:是否存在实数m,使得不等
式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
推荐套卷
(本小题14分)已知f(x)=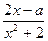 (x∈R)在区间[-1,1]上是增函数,
(x∈R)在区间[-1,1]上是增函数,
(1)求实数a的值组成的集合A;
(2)设关于x的方程f(x)= 的两个非零实根为x1、x2。试问:是否存在实数m,使得不等
的两个非零实根为x1、x2。试问:是否存在实数m,使得不等
式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.