(8分)某经销店为厂家代销一种新型环保水泥,当每吨售价为260元时,
月销售量为45吨,每售出1吨这种水泥共需支付厂家费用和其他费用共100元.该
经销店为扩大销售量、提高经营利润,计划采取降价的方式进行促销,经市场调查
发现,当每吨售价每下降10元时,月销售量就会增加7.5吨.
(1)填空:当每吨售价是240元时,此时的月销售量是 吨;
(2)该经销店计划月利润为9000元而且尽可能地扩大销售量,则售价应定为每吨多少元?
相关知识点
推荐套卷
 y
y +x
+x y
y xy
xy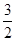 .
. b
b 的次数与单项式
的次数与单项式 x
x y
y

 经过点C,交x轴负半轴于点A.
经过点C,交x轴负半轴于点A.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号