某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目A每次考试成绩合格的概率均为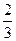 ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为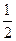 .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响.
(Ⅰ)求他不需要补考就可获得证书的概 率;
率;
(Ⅱ)在这项考试过程中,假设他不放 弃所有的考试机会,记他参加考试的次数为
弃所有的考试机会,记他参加考试的次数为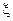 ,求
,求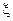 的数学期望E
的数学期望E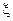 .
.
推荐套卷
某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目A每次考试成绩合格的概率均为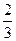 ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为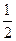 .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响.
(Ⅰ)求他不需要补考就可获得证书的概 率;
率;
(Ⅱ)在这项考试过程中,假设他不放 弃所有的考试机会,记他参加考试的次数为
弃所有的考试机会,记他参加考试的次数为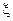 ,求
,求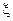 的数学期望E
的数学期望E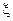 .
.